
V minulém díle představování satelitních navigací jsme skončili ve chvíli, kdy přijímač chytil signál ze satelitu a byl schopen dekódovat navigační zprávu. Dnes na to navážeme, naučíme ho zprávě porozumět, využít ji k výpočtu polohy a zjistit, jak je asi tak přesná. Ukážeme si různé metody zpřesňování měření i vlivy, které na ni mají negativní dopad.
Počítáme polohu
Hrubý nástin je jednoduchý: určíme polohu satelitů, „změříme“ jejich vzdálenosti od přijímače a provedeme něco-jako-triangulaci. Ale jak je vám asi jasné, takhle jednoduché to zase nebude.
Už samotná poloha satelitů je hluboká králičí nora: v navigační zprávě máme efemeridy neboli parametry oběžných drah, ale ty se určují v inerciální vztažné soustavě. Pro popis pohybu satelitů je vhodné na chvíli zapomenout, že se Země otáčí (nebo že tam vůbec je), a zafixovat jen její střed jako hmotný bod. Této soustavě se říká ECI (Earth-Centered Inertial) a je definována tak, že osa Z prochází zemskými póly, osa X spojuje střed Země se vzdálenou hvězdou a osa Y je ortogonálně doplňuje. Má to tu výhodu, že oběžné dráhy satelitů tu jsou konstantní skoro-kružnice a dobře se popisují a parametrizují.
Z hlediska určení polohy na Zemi je to ale nepraktické, neboť nikoho upřímně nezajímá poloha vůči vzdálené hvězdě, která se navíc každým okamžikem mění. Pozice se proto počítá v ECEF (Earth-Centered, Earth-Fixed) referenčním rámci, který už je nám bližší: osa Z opět prochází póly, osa X vede ze středu Země po průsečík rovníku a nultého poledníku a osa Y je opět doplňuje tak, aby vznikl ortogonální systém. ECEF již není inerciální, neboť se otáčí společně se Zemí.
Postup určení polohy satelitů v ECEF tedy je: podle aktuálního času spočítat polohu satelitů v ECI, provést (časově závislou) transformaci ECI-ECEF a takto vyzbrojeni můžeme postoupit do druhého bodu… Ovšem malý problém: nemáme přesný čas (alespoň pokud počítáme polohu po studeném startu).
Přesuneme se tedy k řešení druhého problému: měření vzdálenosti od satelitu k přijímači. Navigační zpráva v každém sub-frame obsahuje slovo, které má čítač sekund od začátku týdne (GPS Time of Week). Přijímač tak ví, že hrana bitu, kterým toto slovo začíná, přesně odpovídá určitému GPS času. Tak získá hrubý odhad – hrubý protože ona hrana přesně odpovídala danému GPS času v okamžiku vysílání. Signál pak ale cestoval zhruba 60-90 milisekund, než jej přijímač zachytil. Navíc satelity jsou obecně různě daleko od přijímače, takže ten má oněch hran „na výběr“ hodně. Kudy dál?
Důležité je si uvědomit, že čas na satelitech je vzájemně synchronizován, takže ony hrany opouští antény ve stejný okamžik. Rozdíly v přijímači jsou způsobeny různými vzdálenostmi, které musí překonat. Poslední neznámá je rozdíl mezi časem v přijímači a GPS časem – kdyby měl přijímač čas přesně synchronizovaný s GPS, mohl by už v tomto okamžiku vědět přesné vzdálenosti k satelitům, neboť by přesně věděl, jak dlouho jednotlivým signálům trvalo k němu doletět.
Jenže on jej nemá (pomineme nyní přijímače s vlastními atomovými hodinami). Nezbývá nám tak než si „tipnout“ nějaký rozumný odhad, tak aby všechna měření byla v možném rozmezí (každá milisekunda ovšem znamená skoro 300 km chybu). Proto se taky těmto měřením říká v angličtině pseudorange, ne range – protože dopředu víme, že vzdálenost jen odhadujeme na základě dostupných údajů, místo abychom ji přesně měřili.
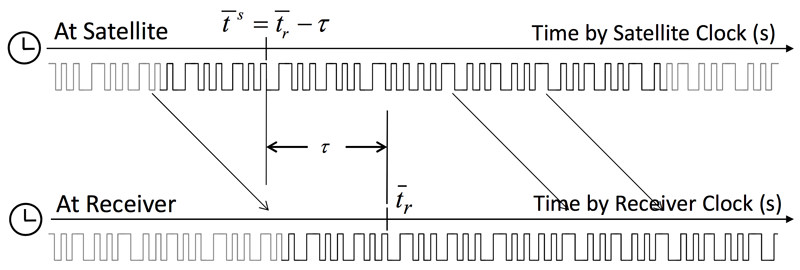
Zjednodušený model pseudorange: vyslaný signál je s určitým (neznámým) zpožděním přijat v přijímači. Vidět jsou jeho složky: jednak τ (rozdíl mezi časem přijímače a časem satelitu), jednak doba letu signálu.
Další, co budeme potřebovat, je odhad vlastní polohy přijímače, tak abychom mohli spočítat očekávané vzdálenosti a porovnat je s naměřenými. Pokud nemáme nic lepšího (což v našem obecném případě nemáme), zvolíme střed Země jakožto místo s nejmenší nejhorší možnou chybou. Výsledkem tohoto kroku je vektor Δρ (delta pseudorange), čili rozdíl mezi tím, kolik by měla být vzdálenost od přijímače k satelitům, pokud byl náš odhad správný, a tím, co jsme skutečně naměřili/odhadli.
Už se blížíme ke konci: nyní máme ECEF polohy satelitů, ECEF odhad polohy přijímače a můžeme pro každý satelit spočítat jednotkový vektor od přijímače k satelitu (logicky taky v ECEF). Když si tyto vektory (dejme tomu, že jich je n) napíšeme do řádků matice, dostaneme n×4 matici zvanou geometrická a značenou G nebo H, dle literatury a vkusu autora. Několika maticovými výpočty vykouzlíme nejmenší čtverce a vypustíme je na náš vektor Δρ: [(G^T×G)^{-1}×G] × Δρ = e. Proč nejmenší čtverce? Je to metoda optimální v tom smyslu, že maximalizuje podmíněnou pravděpodobnost, že spočtená poloha je správná za předpokladu naměřených pseudorange. Výsledek výpočtu je e neboli error vector – čili vektor, který opravuje náš úvodní odhad polohy a času.
Odteď se budeme už jen opakovat – opravíme si odhad polohy, posuneme hodiny v přijímači podle hodnoty v e a znovu zopakujeme celé kolečko s výpočtem polohy satelitů (změnil se nám čas a při orbitální rychlosti necelé 4 km/s hraje roli každá milisekunda), transformace z ECI do ECEF, výpočtu Δρ a nejmenších čtverců. Spočtená poloha obvykle poměrně rychle konverguje: další výpočty se zarazí, pokud norma error vectoru klesne pod nějakou hranici anebo proběhne maximální počet výpočtů – to třeba v případech, kdy geometrie nestojí za nic a poměr signálu k šumu taky není zrovna hvězdný, a tak by norma error vectoru pod stanovenou hranici nemusela klesnout nikdy. Pak se holt poslední spočtená poloha označí za správnou, aby se přijímač nezacyklil.
Toto cvičení se opakuje s železnou pravidelností každou sekundu (nebo jak často přijímač polohu počítá). Později je již vše rychlejší, neboť odhad polohy je poměrně přesný (nikdo se za sekundu nepřesune na druhý konec světa), čas je taktéž správně zarovnán a konvergence je na jeden-dva výpočty.
Chyby pseudorange
Hurá – máme spočítanou polohu! Až na to, že postupem výše by nám konzistentně ukazovala přinejlepším cokoliv v okruhu desítek metrů. Ale proč?
Zaměřme se prvně na přesnost jednotlivých pseudorange. Jaké jsou negativní vlivy, které nám do nich vnáší chybu?
Prvně tu je část, kterou můžou ovlivnit provozovatelé GNSS, tzv. Signal-in-Space: sestávající z chyb hodin a efemerid. Prvně jmenovaná vzniká nedokonalou synchronizací hodin v jednotlivých satelitech (vždy tam bude určitá malá chyba), druhá zase nedokonalými parametry drah, které tím pádem „posunou“ satelit o kousek jinam oproti skutečnosti. Obojí závisí čistě na provozovatelích a jejich designu celého systému, pozemním segmentu atp. To je taky hodnota, kterou se trumfují zástupci GPS a Galilea na konferencích – už několik let je v obou případech v řádu nízkých desítek centimetrů.
Tady trochu odbočím: přesné efemeridy satelitů se určují numericky z naměřených hodnot. K tomuto účelu mají GPS i Galileo po celém světě rozeseté sledovací stanice (jak se hodí mít vojenské základny nebo bývalé kolonie všude možně), které přirozeně znají svou polohu, sledují všechny satelity a počítají, jak přesné jejich signály jsou. V obou případech je pokrytí prakticky celosvětové a z naměřených dat se dají aproximovat efemeridy tak, aby výsledná chyba v poloze satelitu byla jednak co nejmenší, jednak aby nikde na světě „neustřelila“. Efemeridy se dají počítat průběžně a aktualizovat klidně několikrát za den, tak, aby „okno“ aproximace nemuselo být moc dlouhé (když si zkusíte spočítat polohu satelitu s čerstvými efemeridami během dvou-tří dnů, a srovnat ji s polohou spočítanou pomocí efemerid zafixovaných na začátku tohoto intervalu, tak poměrně rychle po jejich expiraci chyba strmě roste, klidně desítky/stovky metrů).
Fakt, že GPS mělo i historicky sledovací stanice rozprostřené po celé Zemi (byť skutečně celosvětové pokrytí je záležitost až posledních let), byla velká konkurenční výhoda oproti GLONASSu – ten měl svoje stanice umístěné výhradně na území bývalého SSSR. Nad ním tedy věděl poměrně dobře, co se se satelity děje, ale na druhé straně světa byli ruští inženýři slepí a mohli pouze doufat v nejlepší. Proto byl GLONASS v blízkosti bývalého SSSR poměrně přesný, kdežto ve zbytku světa mohlo být lepší se mu vyhnout. Součástí rekonstrukce GLONASS v posledních patnácti letech je i rozšíření pozemních stanic jednak recipročně s Čínou, jednak do spřátelených zemí jako Brazílie, Nikaragua, Venezuela či JAR. Trochu kuriózně je několik stanic i na Antarktidě. Tím GLONASS získal mnohem lepší přehled o svých satelitech a mohl zpřesnit svoje efemeridy pro většinu světa.
Vraťme se k chybám pseudorange: ve volném vesmíru činí pár desítek centimetrů (95 %), ale do cesty se mu pak zlomyslně postaví ionosféra: rádiový signál je při jejím průchodu malinko zpomalen, což přeloženo do řeči vzdálenosti přidává chybu kdekoliv do řádu metrů. Běžně je chyba kvůli ionosféře dominantní, proto vznikl i její model (Klobuchar), který se tuto chybu snaží modelovat v závislosti na poloze přijímače a satelitu (tj. např. pod jakým úhlem signál prochází ionosférou a v jakém bodě). Vysvobozením ale bylo až zavedení dvou civilních frekvencí (pásma L1 a L5) – ionosféra totiž rádiový signál zpomaluje v závislosti na jeho frekvenci. Když tedy satelit vysílá oba signály současně a přijímač je oba úspěšně sleduje, z rozdílu časů jejich přijetí dokáže dovodit ionosférickou chybu a téměř kompletně ji odstranit (zůstane jen chyba druhého a vyšších řádů, která je ale oproti chybě prvního řádu zanedbatelná). Jak uvidíme v příštím díle, toto je killer feature nových generací GNSS.
Na okraj: Klobucharův model není jediný. Před lety vznikl z evropských fondů další model: Nequick. Vyznačoval se tím, že byl nesmírně složitý, jeho výpočet trval neúměrně dlouho a zlepšil výsledky sice znatelně, ale nikterak dramaticky. Snahy prosadit ho kromě výzkumu i do praktických přijímačů se ale naštěstí setkaly se zděšením a úspěšným odporem, protože tu věc včas nespočítal ani výkonný PC.
K ionosféře se ještě váže jeden jev, se kterým si nikdo pořádně neví rady: scintillation (nevím o českém ekvivalentu). Ve zkratce jde o to, že při vysoké sluneční aktivitě se kolem rovníku tvoří poměrně velké oblasti ionosféry s velmi vysokou koncentrací nabitých částic, které tím pádem více zpomalují procházející signál. To by samo o sobě nebylo tak hrozné, holt by se chyba v pseudorange musela buď odhadnout a opravit, anebo by se o ni do jisté míry postaraly nejmenší čtverce; horší je, že tento jev je velmi dynamický. Signál tedy prudce „zpomaluje“ a zase „zrychluje“, což trackovací smyčce nedělá dobře a snadno ho pak dočasně ztratí. Dvě frekvence tu slouží spíš jen jako redundance, kdyby se náhodou aspoň jedna udržela, tak měření ze satelitu není zcela ztraceno. Dobré je, že tyto oblasti nejsou příliš rozsáhlé a zabírají poměrně malou část oblohy, takže přinejhorším přijímač odepíše několik satelitů (proto je dobré jich sledovat dostatečnou rezervu a ideálně i z více systémů). Jak může scintillation vypadat, je vidět např. tady nebo tady.
Další překážkou, kterou musí signál překonat, je troposféra. Ta signál zpomaluje pro změnu interakcí s plyny, a to jak dusíkem a kyslíkem, tak vodními parami. Ty první mají na svědomí drtivou většinu chyby, která je ale stabilní (stejně jako obsah dusíku a kyslíku ve vzduchu). Ty druhé jsou výrazně proměnlivější (srovnejte vlhkost vzduchu třeba v tropech a na pouštích), ale zase vodních par je ve vzduchu poměrně málo, a tak velmi proměnlivá a špatně modelovatelná část chyby ani v nejhorším případě nenadělá velkou paseku.
Pak už zbývá jen přijímač: o což se postará třeba termální šum a nepřesnost sledování autokorelační špičky primárních kódů. Trackovací smyčka se na ní snaží udržet pomocí tří korelátorů – jeden je nastaven na předpokládanou špičku a další dva s určitým odstupem před ní a po ní (proto se jim říká early, prompt a late). Z porovnání hodnot, které korelátory „nasbírají“, se pak domýšlí, kde je skutečná špička a příslušně se pro příští běh smyčky lokální kopie signálu posune. Vzpomeňme si na tvar špičky BPSK z minula, že její strany jsou poměrně mírně svažité, a když se k tomu přidá šum, udržet se skutečně blízko vrcholu není nic snadného. O trochu lepší to má BOC modulace použitá v Galileo E1, tam se ale zase musí pracovat lépe s pěti korelátory (přidáme i very early a very late), neboť autokorelační funkce není prostá a nemuseli bychom ze tří hodnot jednoznačně určit, kde se na ní nacházíme.
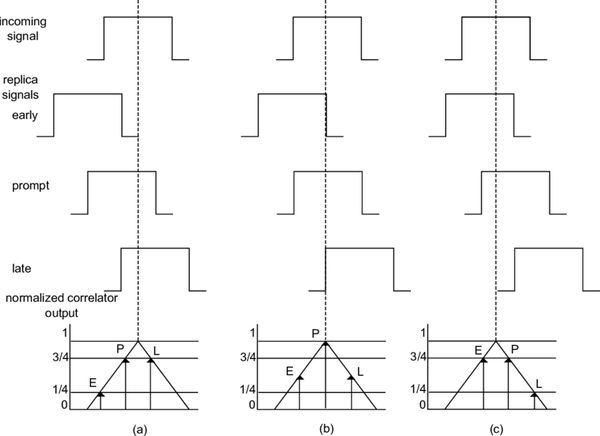
Tři scénáře trackingu: (a) signál v přijímači předchází přijatý, (b) přesně zarovnaný, (c) opožděný. Vidět jsou také hodnoty naakumulované v early, prompt a late korelátorech, a jak se z nich dá odhadnout potřebná oprava.
Problém sledování přesné špičky je umocněn tím, že přijímač si nemůže lokální kopii kódu posunovat spojitě dle libosti, ale jen diskrétně v rámci „tiků“ své základní frekvence, což vnáší další chybu typicky v řádu centimetrů. Při zašuměné autokorelační funkci je snadné se posunout o kousek chipu vedle – a pamatujte, jeden chip je 1/1023 milisekundy, čili chybné určení špičky o pouhou setinu chipu znamená skoro třímetrovou chybu.
V tento moment už máme slušné ponětí o chybách, co rádiový signál „posbírá“ cestou až do přijímače, ale kdybychom to implementovali takto, pořád by nám ve výsledcích poloha lítala o desítky metrů mimo. Jak to?
Dobrý den, pane Einsteine
Do plejády fyziků, které při poznávání GNSS potkáváme, se totiž zařadil i ten patrně nejznámější – Albert Einstein – se svou teorií relativity. Orbitální rychlost satelitů je sice pouze zhruba 0,001 % rychlosti světla, ale to už stačí, aby vliv na palubní hodiny byl měřitelný a ty se každý den o zhruba 7 mikrosekund zpozdily. Opačným směrem působí fakt, že ve slabším gravitačním poli než na povrchu Země hodiny pro změnu zrychlují, a to zhruba o 46 mikrosekund za den. Dohromady bychom tak při pohledu ze Země pozorovali zrychlení hodin o zhruba 38,6 mikrosekund. Tyto efekty nicméně může (a musí) opravovat přímo provozovatel systému tím, že palubní hodiny místo 10,23 MHz syntetizují malinko nižší základní frekvenci: 10,22999999543 MHz. Při pohledu ze Země se jeví tak, jak přijímače očekávají.
S čím už si musí poradit přijímač sám, je Sagnacův efekt. Protože pozice satelitů počítáme zprvu v ECI, který je inerciální, a pak je převádíme do ECEF, který neustále rotuje, zdánlivé dráhy, které signál musí urazit, nejsou přímky, ale křivky. Jejich délka se buď natahuje, nebo zkracuje – to podle toho, jestli signál letí po směru rotace nebo proti němu. Pokud bychom toto nebrali v potaz, chyba v naměřených pseudorange by dosahovala desítek metrů, průměrně kolem padesáti.
Fajnšmekři si ještě namodelují Shapirův efekt, neboť rádiový signál v blízkosti hmotných objektů jako je Země je ovlivněn zakřivením časoprostoru – ale pokud se na to vykašlete, dostanete asi 2cm chybu. Toto má smysl hlavně pro geodetické a vědecké přístroje.
Po započítání všech těchto vlivů už dostaneme zhruba to, jak to v 70. a 80. letech Američané vymysleli, jak si mysleli, že to asi bude přesné (a proč taky byl jejich vojenský signál navržen s desetinásobnou frekvencí, a tedy i desetkrát lepší přesností) a proč podle mnohých mýtů a legend dal Pentagon zelenou zpřístupnění civilnímu sektoru.
DOP a geometrie
Zatím jsme se zabývali tím, jak jsou asi přesné pseudorange, ale uživatele stejně zajímá hlavně to, jak je přesná jejich výsledná poloha. Vzpomeňme si na výpočet polohy pomocí geometrické matice, a jeden mezivýsledek: (G^T×G)^{-1} = C. Tato čtvercová matice C se nazývá kovarianční a zajímají nás prvky na diagonále – při dodržení všech konvencí je první prvek σ^2(x), druhý σ^2(y), třetí σ^2(z) a poslední σ^2(t). Čili variance podle jednotlivých os i času. Jaký to má geometrický význam?
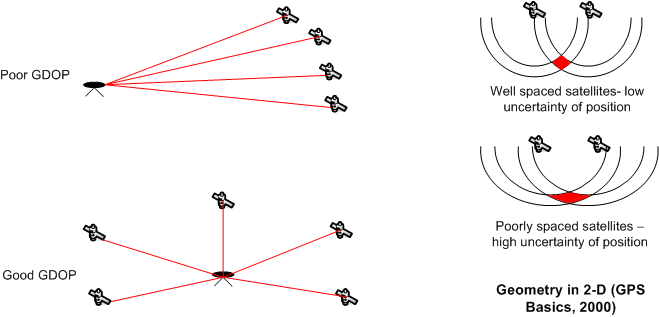
Z obrázku je patrné, co se míní „dobrou“ a „špatnou“ geometrií. Pseudorange z každého satelitu můžeme nějak naměřit, ale počítáme i s chybou, která se běžně modeluje Gaussovým rozložením s nějakou standardní odchylkou (její složky jsme si uvedli dříve). Takže pro oblast jedné sigma (tj. pravděpodobnost cca 68 %) vlastně dostaneme mezikruží, a to pro každý satelit. Když uvážíme pouze 2D případ a úhel mezi vektory k satelitům bude velmi ostrý, vzniklý průsečík obou mezikruží bude v jednom směru úzký a v druhém dlouhý. Právě v tom „dlouhém“ směru pak máme mnohem větší nejistotu v pozici než v tom „úzkém“, a proto je taková geometrie „špatná“. Naopak kdyby vektory k satelitům svíraly pravý úhel, mezikruží se nám protnou ideálně a v každém směru bude nejistota (stejně) malá.
V prostoru to je o trochu složitější: jednak nejde o mezikruží, ale „mezikoulí“, jednak jednotlivých vektorů je mnohem víc než dva. Vzniklý útvar tak má v osách x, y a z standardní odchylky popsané sigmami na diagonále kovarianční matice. A teď už si můžeme také konečně vysvětlit kritérium DOP<6: jako DOP (nebo též PDOP) se běžně označuje odmocnina ze součtu prvních tří prvků na diagonále – čili standardní odchylka maximálního rozměru průsečíku všech mezikoulí. Geometricky řečeno, tento průsečík (který nám určuje oblast, kde je s pravděpodobností cca 68 % správná poloha) není v žádném směru větší než DOP (Dilution of Precision; PDOP znamená Position Dilution of Precision, čistě protože je definovaný i VDOP – vertikální, HDOP – horizontální a GDOP – všechny prvky na diagonále, včetně standardní odchylky času).
Teď už by snad mohlo být jasné, proč se DOP použije jako měřítko kvality geometrie, že někde se musela nakreslit čára mezi dostatečnou a nedostatečnou kvalitou a jaký to asi tak má význam. Akorát teď na DOP zase zapomeneme, protože se už dávno prakticky nepoužívá.
DOP měl totiž význam hlavně v době, kdy všechny satelity měly stejnou nebo velmi podobnou standardní odchylku pseudorange – a ta byla způsobena umělým znepřesněním, známým jako Selective Availability (SA). Tento mechanismus do civilního signálu přidával pseudonáhodnou chybu o sigma 33 metrů (!), právě aby GPS nebylo přesné až moc. Je snadné ověřit, že tak brutální umělá chyba prakticky překryla všechny ostatní a nemělo příliš smysl se jimi zabývat – stačilo uvažovat sigma 33 metrů.
Jenže v roce 2000 byla Selective Availability nadobro vypnuta a najednou se mezi satelity objevily rozdíly – už kvůli ionosféře, kvůli rozdílně přesným hodinám na palubě různých generací satelitů apod. V ten moment začalo mít smysl zkusit místo nejmenších čtverců použít vážené nejmenší čtverce, v tomto smyslu malinko poupravit maticovou rovnici a získat mj. kovarianční matici vzniklou tím, že přesnějším měřením je dána vyšší váha.
Tento stav trvá dodnes (proto např. satelity, které vysílají na dvou frekvencích, mají ve výpočtu výrazně vyšší váhu než ty jednofrekvenční – protože jejich sigma pseudorange je menší o celou chybu ionosféry) a již se blížíme finálnímu určení statistické přesnosti spočtené polohy.
Ta je typicky uváděna v samostatné horizontální a vertikální složce – z kovarianční matice spočítáme z diagonály sigmu pro horizontální rovinu a vezmeme sigmu pro vertikální osu. Přesnost (accuracy) je definována jako 95% oblast Gaussova rozdělení – proto stačí horizontální i vertikální sigmu přenásobit 1,96 a máme statistickou oblast (válec) okolo spočtené polohy, kde je s 95% pravděpodobností ta skutečná.
Hurá.
Protože se článek už neúměrně protáhl, zbytek pojednání o zpřesňování polohy a dalších moderních vychytávkách bude následovat zase příště.
16.02.2025 zajíc
Související články:
- GNSS na Měsíci: nesourodé povídání o satelitních navigacích (16.3.2025), zajic
- Posloucháte v rádiu dopravní zpravodajství? A bylo vám to někdy k něčemu? (21.10.2018), 156
7 163x přečteno







 (170x známkováno, průměr: 1,10 z 5)
(170x známkováno, průměr: 1,10 z 5)