
Tímto článkem bych chtěl podat čtenářům špetku z teorie her aplikovanou na dopravní systém. Auta se tady probírají docela často a podrobně, v tomto článku chci ukázat, co dostaneme, když je hodně aut pohromadě.
Budu se snažit použít co nejméně matematiky (přemíra matematických symbolů prý to čtenáře odrazuje). Cílem není vyložit celou teorii najednou, spíš upozornit na zajímavá fakta a pobídnout k dalšímu samostatnému bádání.
Nashova rovnováha
Začnu pojmem Nashova rovnováha. Je to pojem, na který v teorii her narazíte téměř okamžitě. Podle názvu se čtenář dovtípí, že je pojmenován po Johnu Nashovi. Definice Nashovy rovnováhy je vcelku prostá a intuitivní, hodně neformální definice by byla asi tato:
Pokud žádný z hráčů nemůže zvýšit svůj zisk tím, že změní jednostranně (tj. ostatní nezmění) svou strategii, je hra v Nashově rovnovážném bodě.
Přesnější (formálnější) definice najdete třeba na wikipedii (nebo v pracích Johna Nashe).
Nashova hlavní zásluha je v tom, že dokázal, že pro každou hru s konečným počtem hráčů a strategií existuje rovnovážný bod ve smíšených strategiích (něco o smíšených strategiích si lehce najdete na internetu, tady s tím nechci zdržovat, v tomto článku se bez nich obejdete). Stalo se tak v celkem nenápadném článku, který vyšel v roce 1951 (a předtím ještě jeden v roce 1950).
Hra může mít i více rovnovážných bodů. V definici se nic neříká o výši zisku pro jednotlivé hráče, zisk nemusí být pro všechny hráče stejný. Dokonce ani není jasné, zdali se k této rovnováze hra dopracuje. Za určitých docela přirozených podmínek (které je ale někdy v praxi obtížné splnit) se dá dokázat, že iteračně se k nějaké rovnováze hráči dopracují.
Zatímco v teorii se o rovnovážném bodě pěkně mluví, v praxi je to poněkud horší, protože život je složitější, než nějaká hra. Člověk většinou nemá dost informací, nechová se úplně racionálně, případně jinak či špatně odhaduje zisk své strategie (např. když obyvatel Brna volí v krajských volbách ČSSD s vidinou „odpuštěných“ poplatků v lékárně – v Brně není jediná krajská lékárna). Ale jsou situace, kde se teorie her dá aplikovat docela dobře. Prvním kouskem, který chci ukázat je Braessův paradox.
Braessův paradox
Prof. Dr. Dietrich Braess působí na „Fakultät für Mathematik Ruhr-Universität Bochum“ (tohle jsem se bál přeložit). V roce 1968 publikoval článek, kde uvádí skutečný příklad, kdy po rozšíření dopravní sítě došlo proti očekáváním ke zhoršení dopravní situace (prodloužení jízdní doby). Tento jev se dá vysvětlit právě na základě Nashovy rovnováhy. Původní článek (v němčině) i anglický překlad jsou k dispozici na univerzitních stránkách prof. Braesse. Samozřejmě existuje i opačný jev, kdy se po odebrání spojnice jízdní doba sníží (našel jsem jenom zmínku tohoto znění: „Earth Day 1990 – NYC closed 42nd street. Many were worried, actually improved.“, ale nikde jsem nenašel mapku).
Demonstrace Braessova paradoxu
Pro jednoduchost předvedu zcela umělý příklad s nereálnými číselnými hodnotami, aby paradox více vynikl (tento příklad se stejnými čísly najdete u mnoha autorů, takže ani nevím, kdo s ním přišel první). V reálu nevychází rozdíl tak divoce, ale je tam.
Představme si, že z místa A do místa B jede každé ráno 1000 aut. Mají k dispozici 2 trasy, přes místa C a D. Jízdní doba na jednotlivých úsecích může záviset na tom, kolik aut po trase jede (i tento předpoklad je v praxi lehce nereálný, protože první auto projede bez zdržení, zdrží se až auta za ním). Viz pokus o ASCII art.
_____ x/1000 _____
-------- | C | -------------------- | B |
/ ----- -----
1 / /
/ 1 /
/ /
_____ x/1000 _____ /
| A | ----------------------- | D | --------
----- -----
V úsecích AC a DB je jízdní doba 1 jednotka (třeba hodina) bez ohledu na počet vozidel (představte si např. mnohaproudovou silnici). Naopak v úsecích CB a AD je jízdní doba úměrná počtu vozidel označenému x (to by byla nějaká úzká klikatá silnička).
Nedá moc práce zjistit, že Nashův rovnovážný bod je ve stavu, kdy půlka aut (tj. 500) využije horní cestu ACB a druhá půlka spodní cestu. Tento bod je zároveň „společenským optimem“ v tom smyslu, že minimalizuje součet jízdních dob všech aut, ale to sem až tak nepatří. Jízdní doba je v tomto případě 1,5 jednotky.
Podívejme se na situaci, kdy nějaká hlava prosadí nápad, že přidá spojnici CD s nulovou jízdní dobou (to je samozřejmě nereálné, ale pro jednoduchost necháme nulu. Představte si třeba most přes řeku nebo tunel pod skalním masívem, pár stovek metrů je mizivých ve srovnání např. s 50km). Nedá moc práce zjistit, že původní rovnováha už není rovnováha, když řidič ze spodní trasy ADB zvolí trasu ADCB, určitě si pomůže. Způsobí tak prodloužení jízdní doby na horní cestě ACB, takže postižení řidiči začnou volit jinou strategii.
_____ x/1000 _____
-------- | C | ==================== | B |
/ ----- -----
1 / /
/ 0 1 /
/ /
_____ x/1000 _____ /
| A | ======================= | D | ---------
----- -----
Nakonec se rovnováha posune do stavu, kdy všichni zvolí cestu ADCB (na obrázku zdvojená). Jízdní doba tentokrát vyjde 2 jednotky, čili 4/3 původní doby (obzvláště to naštve řidiče, kteří projíždějí úsekem AD nebo CB někam mimo obrázek a je jim docela volné, jak se dohodnou řidiči jedoucí z A do B).
(Poznámka 1: číslo 4/3 nevyšlo náhodou. Pokud ve vzorci pro jízdní dobu vystupuje x nanejvýš v první mocnině (tady to je x/1000), je to největší možná hodnota. Pro vyšší mocniny x toto maximální číslo vyjde větší. Bližší podrobnosti např. v doktorské práci Tima Roughgardena, viz odkazy).
Z tohoto příkladu je vidět, že Nashova rovnováha nemusí být optimální (ale to byste se dočetli už v článku o Nashově rovnováze na wikipedii).
Zdánlivý paradox je v tom, že přidáním možnosti volby se situace zhorší. Člověk by čekal, že když ke stávajícím možnostem dostane další volbu, může si jenom polepšit.
Downs–Thomsonův paradox
(Též známý jako Pigou-Knight-Downs paradox)
Teď z jiného soudku. Z města A do města B dojíždí množství lidí do práce. Dopravovat se můžou buďto vlakem nebo individuálně autem. Čistá jízdní doba (ode dveří ke dveřím) je řekněme 40 minut vlakem a 30 minut autem. Z nějakého důvodu se stane, že jízdní doba vlaku se zvýší (třeba nějaká reorganizace, nové vedení apod.) na 50 minut. To povzbudí některé cestovatele k přechodu od vlaku k autu. Následkem toho se ale zhorší dopravní zácpy na silnici, takže jízdní doba autem se prodlouží na 40 minut. Ovšem vlakový dopravce teď má prázdnější vlaky, takže se rozhodne prodloužit intervaly mezi vlaky, takže jízdní doba vlakem se protáhne na 60 minut, což ovšem povzbudí další cestovatele k přechodu na automobilovou dopravu. Silnice je přeplněná a jízdní doba se zvýší na 50 minut. V tomto bodě zasáhnou politici, kteří si libuji ve stříhání pásek a nechají stávající silnici rozšířit (nebo postavit úplně novou). Jízdní doba se tak zkrátí na krásných 30 minut. Další část lidí z vlaku se přesune k automobilu, takže na silnici je opět boží dopuštění a jízdní doba trvá 50 minut (za celou tu dobu se cestovatelům změnila jízdní doba z původních 30/40 minut na 50/60 minut, v tomto případě zcela záměrně vyšlo, že autem to nakonec trvá déle, než předtím vlakem).
Shrnutí je v následující tabulce:
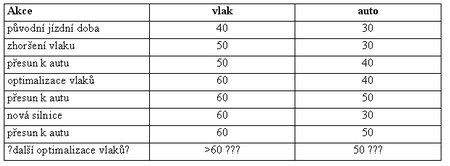
V obou případech je výsledek ten, že se utratila spousta peněz za rozšíření silniční sítě, a situace se zhoršila.
Jak těmto paradoxům předcházet
Pokud si dobře pamatuji, tak jsem viděl nějaká kriteria na detekci Braessova paradoxu v práci Tima Roughgardena (viz odkazy dole, mimochodem, měl to moc pěkně zpracované), ale byla to spíš akademická diskuse. Když dáte v Google hledat „detect braess paradox“, vypadne hromada článků. V jednodušších případech by mělo být možné detekovat hrozbu Braessova paradoxu i bez velké vědy. Stejně jako v jiných oblastech i tady platí, že by člověk měl jednat s rozmyslem.
Pokud jde o Downs–Thomsonův paradox, tak nevím, žádné přesné kritérium jsem nenašel. Vzhledem k množství vlivů to asi nebude jednoduché. Náprava asi není tak jednoduchá, protože je těžší přesvědčit lidi, aby přesedlali z auta na hromadnou dopravu. Navíc ne všichni se bez auta obejdou (představa instalatéra, jak si vozí materiál vlakem je trošku mimo).
Mimo rámec článku je otázka, kolik investic do veřejné dopravy je ještě efektivních a kdy už zvýšené náklady nepřinášejí užitek.
V obou ukázaných případech paradoxů je smůla, že větší množství lidí se asi není schopno domluvit na společné strategii a pak ji dodržet (např. nepoužívat spojnici CD). Pár takových experimentů jsme zažili a nedopadlo to úplně dobře.
Braessův paradox může nastávat například i v počítačových sítích, ale zatím se s ním daří bojovat, nejspíš i proto, že rychlost linek ještě stále rychle roste (vysílání-nevysílání olympiády po internetu byl v podstatě lokální problém).
Náměty na další čtení
V jednom článku se nedá popsat všechno, pro zvídavé uvádím pár námětů na související témata. Kdybyste moc chtěli, možná bych napsal nějaký další článek, ale už by to bylo trochu složitější čtení, objevily by se tam matematické symboly.
Známé a zajímavé příklady Nashovy rovnováhy
·







 (6x známkováno, průměr: 4,33 z 5)
(6x známkováno, průměr: 4,33 z 5)